
NIERBO HDMI Switch, HDMI 4K Switcher Duplicator Supports 1080p Full HD 3D, 3-Port with USB Power Cable for TV, BLU-Ray, Cable Box, PS3 / PS4

Amazon.com: USB C KVM Switch 4K@60Hz, USB C Switcher for 2 Computers Share 1 HDMI HD Monitor and 4 USB Devices, with 100W Power Delivery, USB-C Switch with USB-C Cable, HDMI 2.0

Navceker HDMI 2.1 KVM Switch 4K 120Hz HDMI USB 3.0 KVM Switch USB 8K 60Hz 1080@240Hz USB KVM Switcher HDMI with USB 3.0 port PC
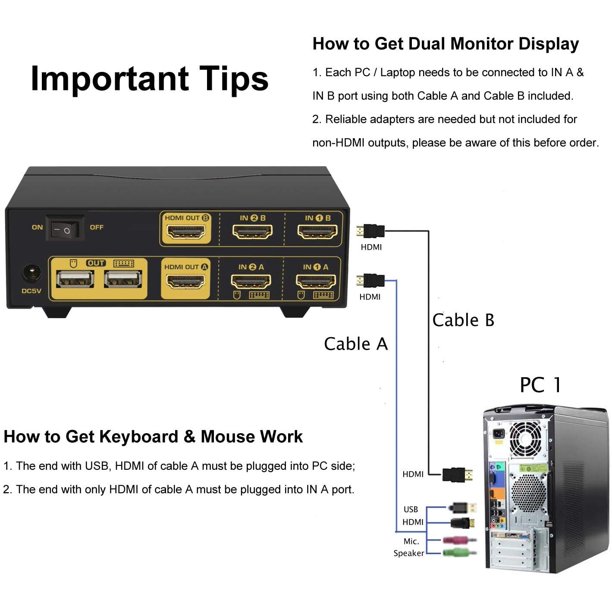
HDMI KVM Switch 4 Port Dual Monitor Extended Display, CKL USB KVM Switch HDMI 4 in 2 Out with Audio Microphone Output and USB 2.0 Hub, PC Monitor Keyboard Mouse Switcher 4K@30MHz

Dual Monitor Kvm Switch Hdmi-compatible Usb 3.0 Switcher Extended Controls For 2 Computer Laptop Share Keyboard Mouse Printer - Audio & Video Cables - AliExpress

Amazon.com: USB 3.0 Dual Monitor KVM Switch HDMI+Displayport 4K@60Hz,2K@120Hz,Camgeet 2 Monitors 2 Computers KVM Switch for 2 Computer Share 2 Display and 4 USB3.0 Devices.Wired Remote and 4 Cables Included : Electronics

Monoprice 4K 2x1 HDMI 1.4 & USB 2.0 KVM Switch, Includes USB 2.0 Data Connection With Over Current Detection And Protection - Walmart.com















